Tutorial 2 – Bayesian inference
In this tutorial we use Fesslix for Bayesian inference.
As method to perform the inference we employ BUS-SuS
(BUS: Bayesian Updating with Structural relaibility methods [1];
SuS: Subset Simulation [2] ).
We investigate the two-degree of freedom problem discussed in [1] (It is a two-story frame structure that is represented as a two-degrees-of-freedom shear building model). The two stiffness coefficients of the model are considered uncertain. The selected two-dimensional prior distribution represents the normalized stiffness coefficients (stiffness coefficients divided by 29.7e6 N/m): The prior consists of two independent log-Normal distributions with modes 1.3 and 0.8 and standard deviation 1.0. The lumped story masses are 16.5e3 kg 16.1e3 kg; and are treated as deterministic. The influence of damping is neglected.
Bayesian updating is performed based on the measured first two eigen-frequencies of the system: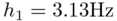
and 
.
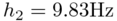The likelihood function of the problem is expressed as:
We investigate the two-degree of freedom problem discussed in [1] (It is a two-story frame structure that is represented as a two-degrees-of-freedom shear building model). The two stiffness coefficients of the model are considered uncertain. The selected two-dimensional prior distribution represents the normalized stiffness coefficients (stiffness coefficients divided by 29.7e6 N/m): The prior consists of two independent log-Normal distributions with modes 1.3 and 0.8 and standard deviation 1.0. The lumped story masses are 16.5e3 kg 16.1e3 kg; and are treated as deterministic. The influence of damping is neglected.
Bayesian updating is performed based on the measured first two eigen-frequencies of the system:
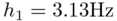and .
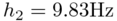The likelihood function of the problem is expressed as:
where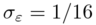 
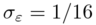and
and
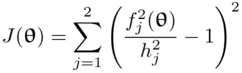
with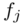 
as the 
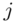th eigen-frequency predicted by the model.
The example problem has a bimodal posterior distribution.
The problem is solved using different numcerical formulations of the likelihood function:
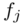as the 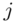th eigen-frequency predicted by the model.
The example problem has a bimodal posterior distribution.
The problem is solved using different numcerical formulations of the likelihood function:
Overview
- Tutorial 2a: Likelihood function formulated directly in Fesslix
- Tutorial 2b: Matlab/Octave likelihood function
- Tutorial 2c: Python likelihood function
- Tutorial 2d: Likelihood function evaluated with external application
Note: Even more interfaces to Fesslix are discussed in Tutorial 1.
The interfaces discussed in Tutorial 1 but not in this tutorial can be transferred
with only minor modifications from Tutorial 1.
References
- [1] Straub D., Papaioannou I. (2015): Bayesian Updating with Structural Reliability Methods. Journal of Engineering Mechanics, Trans. ASCE, 141(3) . dx.doi.org/10.1061/(ASCE)EM.1943-7889.0000839
- [2] Au, S. K., & Beck, J. L. (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Engineering Mechanics, 16(4), 263-277. doi:10.1016/S0266-8920(01)00019-4