Tutorial 1a – Analytical solution
The problem introduced in Tutorial 1 has an analytical solution [1]:
the sum of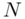 
exponentially distributed random variables follows a Gamma distribution with shape parameter 
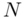and scale parameter 
.
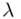Thus, the probability of failure equals the cumulative distribution of the mentioned Gamma distribution evaluated at position 
.
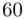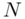exponentially distributed random variables follows a Gamma distribution with shape parameter 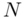and scale parameter .
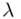Thus, the probability of failure equals the cumulative distribution of the mentioned Gamma distribution evaluated at position .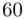
Step by Step Instruction
We start by defining two scalar variables named N and la.
Fesslix parameter file
const N = 100; # number of random variables used in the problem
const la = 1; # parameter of the exponential distribution
const la = 1; # parameter of the exponential distribution
Note: the keyword const defines a scalar variable. The value of such a variable can be changed (i.e., this is not a constant).
Before we actually compute the analytical solution, we output a string:
Fesslix parameter file
echo "The actual probability of failure of the problem at hand is:";
Finally, we evaluate the CDF of the gamma distribution at position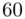 
using the object funplot.
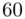using the object funplot.
Fesslix parameter file
funplot cdf( # evaluate the CDF of a distribution
60, # at this position
gamma, # the type of the distribution is 'gamma'
k=N, # the shape parameter
lambda=la # the scale parameter
);
60, # at this position
gamma, # the type of the distribution is 'gamma'
k=N, # the shape parameter
lambda=la # the scale parameter
);
This should return 1.481528e-6 as result.
The complete parameter file
References
- [1] Papaioannou I., Betz W., Zwirglmaier K., Straub D. (2015): MCMC Algorithms for Subset Simulation. Probabilistic Engineering Mechanics, 41, 89-103. doi:10.1016/j.probengmech.2015.06.006